上一篇文章聊了聊「群体智慧」。其中一段提到:
群体智慧的重要前提,是「群体具有一定多样性」。在多样性缺失的群体中,也就是大多数个体受同一类想法影响时,(提取群体智慧的)集成方法不仅难以带来准确度上的好处,还会放大结果的偏差。[……] 更别说在当今无孔不入的社会影响之下,还有过于依赖意见领袖的随大流、以及仅愿在「同温层」表达意见所导致的群体极化等现象了。
当大多数人被某种「错误或无关」的想法干扰时,我们有什么好的对策来提取「掌握在少数人手里的真相」呢?今天分享给大家一组有趣的方法:超预期票决 + 贝叶斯吐真剂。
超预期票决
我们以熟悉的电视问答综艺秀为例。
你是竞答选手,面对一道难题的ABCD四个选项,抓耳挠腮、毫无头绪。于是,你想要使用一次求助锦囊:让现场观众集体投票1。由于题目很偏,观众里真正知晓答案的人极少。在投票的过程中,观众席上有人嘟囔了一句:「遇事不决就选C」,然后你看到一部分人若有所思地点起了头。现在麻烦了。掌握正确答案的人少,而大部分不知所措的人刚受到了「不懂就选C」思潮的影响,所以你完全可以预计到,在最后的投票结果中,C很有可能就是最高票。求助的结果变得毫无意义:你依然不知道该选什么。那现在,该怎么办呢?

倘若「不懂就选C」的思潮没有席卷观众席,那么不管问题再难,只要有少数人持有超越随机乱选的信息量,正常的多数票决就能帮上你:毫无头绪的观众将近乎随机地选ABCD,而剩下少数人投正确答案的概率会稍高一点,他们的这份「小众智慧」有一定可能性突破大众随机投票的底噪,从而在最终结果中体现为最高票。可现在,没有信息量的观众们的投票不再是均匀随机,「选C」的魔咒已然套牢他们的双手,蜂拥而至的C票将淹没真正有用的信息。
聪明的你或许已经想到:要是我们能精确地知道「选C」思潮对观众们造成了多大影响就好了。没有「选C」时,我们对「底噪投票」的估计是均匀随机的「ABCD各25%」。均匀底噪不影响多数票决法的结果,但「选C」的非均匀底噪(或曰「系统性偏差」)则会。假设已知「选C思潮」会使完全不知道正确答案的那些观众做出「A: 10%,B: 10%,C: 70%, D: 10%」的底噪投票结果,那么一个直观的解决方案就自然地浮出了水面:「先用投票结果比例减去这个已知底噪比例,再取最高票」(下面会详细分析这种做法的逻辑)。注意到,直接的多数票决法也等价于「减去均匀底噪后的最高票」,因为均匀底噪对所有选项影响相同,减不减都不改变排序。
可谁又知道「选C」思潮对观众投票比例的具体影响呢?常识上来讲,选C的比例自然比其他会「高一些」,但「高多少」呢?很难估计精确。朋友们,没关系,别忘了上一篇文章的关键结论:
群体智慧的产生需要两个条件:问题的答案可以用常识来猜测,但又难以精确回答;个体的回答具有一定随机多样性。满足以上条件时,群体的平均判断往往能击败个人——甚至专家。
是的,底噪影响的具体数值,我们为什么不请观众们自己来估计呢?
在问「你的选择是什么」的同时,我们不妨再多问一个问题:「你觉得其他人会有多少比例和你一样这么选」。之前,所有观众都听到了那句「遇事不决就选C」,也见证了一部分人的跟随点头。于是,他们对整体投票比例的估计,会考虑到选C思潮的影响。感谢群体智慧,我们将得到一个相对可靠的底噪估计。
收集完所有人的回答,我们便能得到如下形式的统计表格(这里的数据是我编的):
| 答案 | 实际投票比例 | 预测的投票比例(平均值) |
|---|---|---|
| A | 9% | 10% |
| B | 9% | 8% |
| C | 62% | 71% |
| D | 20% | 11% |
单看表格第一列,C拿到了多数票(popular);可是用第一列减去第二列的底噪估计后,你发现,D拿到了超出预期最多的票(surprisingly popular):它比预期的11%足足多拿了9%的票,而其他选项的票数都比预期低。也就是说,C是意料之中的赢家,D则是意料之外的黑马。根据上述「减去底噪后的最高票」逻辑,你最终应该选D。
这种投票/计票法,被称为「超预期多数票决」(Surprisingly Popular Voting)。
在超预期票决系统里,我们在传统的意见征集投票基础上多问了一句:「你觉得其他人会有多少比例和你一样这么选?」。而付出这份额外问答成本的收益就是,我们现在能够在结果中尽量排除「和目标无关、甚至背道而驰的主流因素」。
这是一个非常反直觉的票决方案。上面我用了一个直观的启发式例子,数据全都是编的,你可以不信它真的有效。但这个方法最初由一篇发表在2017年《自然》杂志上的论文提出,有大量实验数据佐证2。
原论文反复使用的例子是「费城是否是宾夕法尼亚州首府」。费城是宾州第一大城市,这是很多美国人熟知的事实;但宾州首府并非费城,而是名不见经传的哈里斯堡。所以对此问题,大多数人的回答都是错误的。下面是51个人回答的真实数据:
| 答案 | 实际投票比例 | 预测的投票比例(平均值) |
|---|---|---|
| 费城是宾州首府 | 66% | 71% |
| 费城不是宾州首府 | 34% | 29% |
按照「超预期票决」(投票比例减去预测比例后取最高),应该选「费城不是宾州首府」(得票34%,比预期的29%要高出5%),而这的确是正确答案。
原论文询问了被试群体七类常识性问题,一共490题,并观察到「超预期票决」的结果正确率比多数投票高出21.3%~35.8%,比按个人信心的加权投票也高出24.2%(见下图)。这个投票法虽反直觉,在统计意义上倒确实给出了更正确的答案。
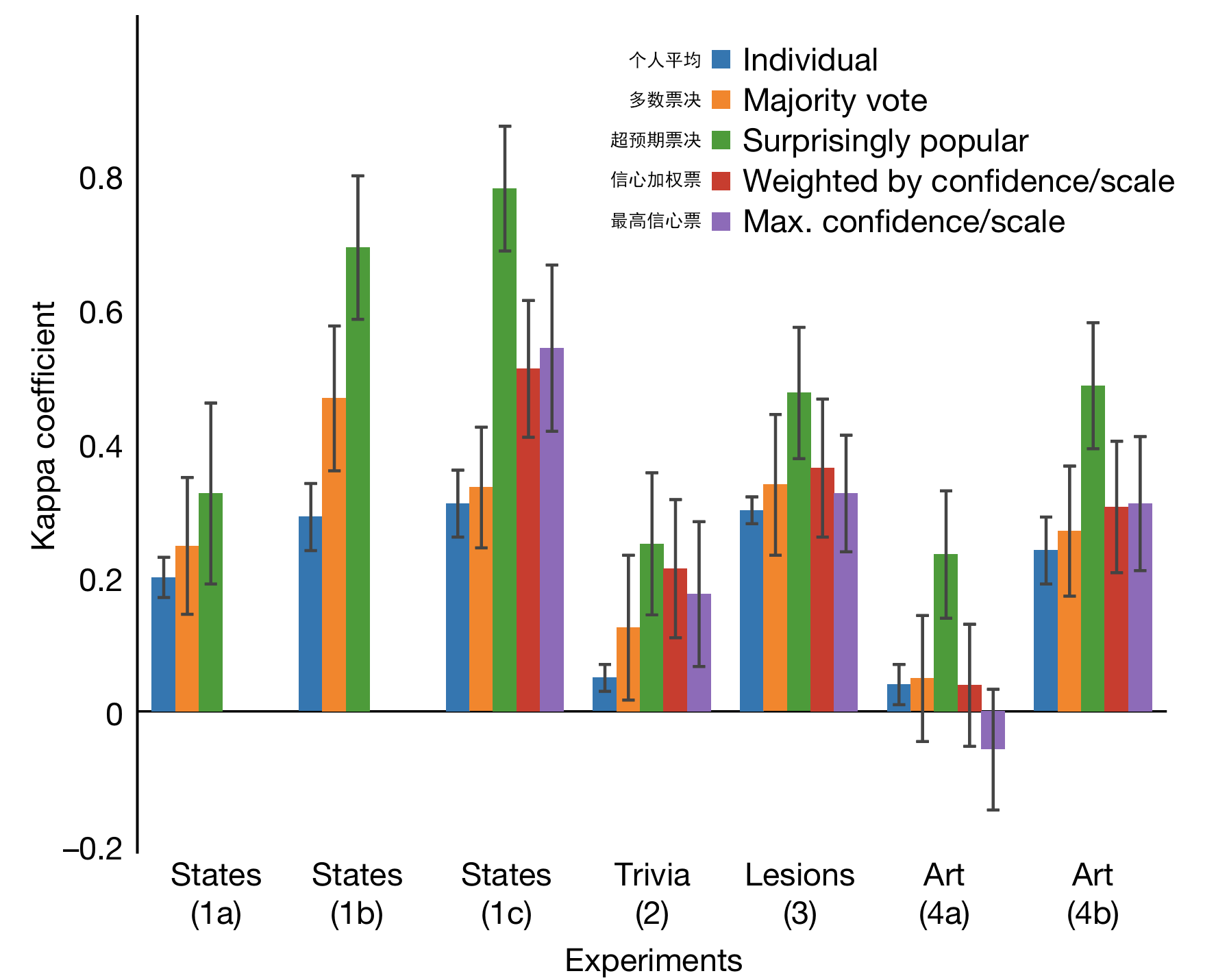
我们现在来仔细分析一下,超预期票决法到底做了怎样的「操作」。
先把投票所蕴含的信息分为两部分:
- A类:与正确答案有关的信息,如「我以前读到过,哈里斯堡才是宾州首府」,「我听某教授讲过,答案好像是D」。
- B类:与正确答案无关或有误导,但会影响整体投票行为的信息,如「费城是宾州最大城市」,「遇事不决就选C」
表格的第一列的票数所含信息是A+B,两类都有。当然,这里假设所有知道A类信息的人都会按其投票,即他们有动力「诚实作答」而不是装傻或捣乱。而表格的第二列,包含的信息介于B和A+B之间。这是因为:
- 不知道A类信息的人,只能预测B类信息对投票的影响。(既然B类信息能影响整体投票,那么自然而然地,绝大多数投票者都应知晓B类信息。)
- 而知道A类信息的人,会有两种极端的边界心理情况:
- 他认为自己是极少数知晓A类信息的专家,而大众对此有盲区,所以他只会预测B类信息对整体的影响
- 他认为所有人和自己一样同时知晓A+B,所以这里他会估计A+B的影响
- 所以表格第二列所反映的信息应在B和A+B之间;当A越稀缺时,这份信息越接近B
所以,用表格第一列减去表格第二列,就相当于在剔除B类信息的影响(同时也误伤了少量A类信息的影响),留下仅和正确答案相关的去噪结果(纯A类信息)。换句话说,「超预期票决」在集成个体答案的同时,排除掉了「大家都知道」的主流信息,以免它误导票决结果,着重去体现那些拥有独家信息的人的真实看法。
当然,如果问题过于简单,那么A类信息亦为所有人所知(即该问题无需专门知识回答),实际投票比例与预测的投票比例就会非常接近,因为两者都是在估计A+B,两列相减后会接近于零。这个现象本身会在投票数据中体现出来,所以可以预设一个阈值,当两列差距小于阈值时,使用只看第一列的多数票决法。这样,即便我们不知道A类和B类信息的比例,也可以使用「超预期票决」法,因为它可以自动回退到多数票决法,至少不会得到比它差的结果。
看上去「超预期票决」似乎非常稳健,适应性颇广。但是在一种特殊情况下,它不但不能纠偏,反而会误导结果。那就是下面这种C类信息存在时:
- C类:与正确答案无关或有误导,但仅影响了一部分人投票行为的信息
具有负面影响力的小众C类信息会导致表格第一列包含A+B+C类信息,第二列则是B到A+B+C之间(因为只有B是大众所知的信息)。这样,超预期票决法不仅无法排除C类信息,还会放大它的整体影响,特别是当A类信息属于大众皆知的常识时:此时第二列在A+B到A+B+C之间,两列一减就只剩C了。
一个简单的C类信息例子:对于判断题「地球是平的,不是圆的」,你认为有多少人会选「同意」?我猜,你心里的估计恐怕是偏低的:据一份2021年对1134名美国成年人的问卷结果,有高达10%的人选择「同意」,另有9%的人选择了「不确定」3……
「地球是平的」这一阴谋论思潮,很少为大众所知,但阴谋论的受众们强烈地相信自己是掌握真相的少数。而「超预期票决」的假设正是「真相掌握在少数人/专家手里」,我们仅需拨开大众的迷雾,便能暴露出真相。真相掌握在所有人手里时,这个方法虽不会更好,但也不会更差。可是,当「特定的错误藏在少数人手里」时,它就会失效并带来负作用。
所以严谨地说,「超预期票决」只是一个提取小众群体意见的集成方法,自动防止主流意见淹没一切。要在怎样的时机运用它,需要斟酌。在很多应用场景里,特别是存在一个可验证的正确答案的时候,C类信息相对罕见,所以「超预期票决」才能在实验和统计意义上战胜传统的多数票决。
贝叶斯吐真剂
很多时候,我们并不是为了追求所谓正确答案,而只是想提取群体的真实想法。
如果自己的意见能够被很快地判定正确错误(如问答、考试),那么大部分人会诚实地、尽力地提交自认为正确答案。但在更多的情况下,人们可能并不愿意发表真实意见。例如下面三种情况:
- 选举投票时,很多小众群体的成员知道自己人微言轻,便会跟票大众,以防之后被歧视排斥
- 采用超预期投票法时,预估整体的投票结果是很费脑子的。所以不少人会图方便地把自己的选项「预测为」100%,或者「预测为」0%以恶意提升自己票数的「超预期性」
- 填写市场调研问卷时,不少人会因爱面子而夸大自己的消费水平和购买意愿,或者仅仅为了获得奖金而随意填写
要怎样做,才会激励群体真实地表达想法呢?答案可能超出了你的预期:「超预期票决」本身就携带了「激励诚实」的核心机制!
附带激励机制的「超预期票决」,最初被称为「贝叶斯吐真剂」(Bayesian Truth Serum)4。方法很简单。我们告诉投票者,在收集投票和预测之后,系统将根据结果给他一定量的(金钱)奖励。奖励多少,与如下指标正相关5:
奖励 = (他所选选项的实际票数 - 该选项的平均预测票数) - K * D(他的预测票数,实际票数)
这个公式奖励你两件事:第一,你的观点是否比大家预想的更受欢迎(诚实表达独特观点);第二,你是否准确看穿了群体的整体想法(准确预测现实)。
先看第二部分。D(他的预测票数,实际票数)是该投票者的预测与实际票数结果的「差距」,差得越远,该投票者获得的奖励就越少。K是一个预设的权重因子。这第二部分测量的是你预测能力的高低,并激励你尽力思考。这解决了上面提出的第二种情况(预测费脑)。
第一部分奖励「你对超出底噪的信息贡献」:
- 如果你是自觉的小众意见持有者(即,你知道自己是小众;这是你能用来在此处谋利的关键信息),那么这部分会奖励你说真话,因为你知道大众的预期很可能会忽略小众的微薄意见,所以你诚实作答除了提高得到有利于你的最终投票结果的可能性,也能同时增加得到的物质奖励。反过来讲,如果你选择不诚实作答,就很可能降低奖励(这部分变为负数)。这解决了上面提出的第一种情况(小众跟票)。
- 在满足一定假设的一般情况下(每个人都依赖理性的贝叶斯后验概率计算预测,并在假设其他人都说真话的前提下做决策,等等),可以证明选择自己心中的选项一定比其他选项在这前半部分所获的奖励高。证明过程较复杂,其正确性依赖于数学形式的选取,核心想法也没有那么直观,本文不做介绍,推荐对严格形式感兴趣的读者阅读原文。这解决了上面提出的第三种最普遍的情况(说真话奖金最高)。
由于贝叶斯吐真剂主张金钱激励,它一般在商业领域应用,例如消费者问卷反馈。如果填写一份问卷便能获得固定的金钱回馈,反馈内容的质量就没有任何保障,一些受访者会为了快点拿到钱而胡乱填写。此时使用贝叶斯吐真剂,告诉受访者他的报酬最终将以该种形式发放,便能够提升回答真实性和预测的精确性。
同一作者在2013年的研究6表明,该方法可以显著降低问卷调查结果中的撒谎/夸大率:从20%-24%降至13%-14%,效果优于让被试当众宣誓不说假话。而且即便不告诉受访者贝叶斯吐真剂的计算机制,仅在一次次问答回合中告知奖金数额,受访者也能潜移默化地领悟到「说真话时奖金高」,从而表现出类似的受激励效果。
综上,「贝叶斯吐真剂」使用了和「超预期票决」相同的机制,激励诚实作答,特别是那些少数专家手里的信息量。
结语
我第一次听说「贝叶斯吐真剂」时,百思不得其解,这是个什么道理?!接着读到同一作者十年后的「超预期票决」,才逐渐领会其中精妙之处。
两种方法的核心都在于,不仅要提取群体中的个体看法,还要提取这些个体对群体本身的看法,并观察两者之区别。这在群体的「共性」和「个性」之间,建立了一个巧妙的二阶自反关系:个体智慧所实际集成的群体智慧,多于个体对群体智慧的估计所集成的群体智慧。群体并非个体所想象的那样是铁板一块,其中蕴含着各类更复杂的小众智慧,亟待发掘。
下次当你想听取他人的独特意见时,不妨试着多问一句:「你觉得其他人会怎么回答?」
上一篇文章讲过,在美国某问答秀节目中,群体智慧现象使得集体投票的正确率高达91%。 ↩︎
Prelec et al., 2017. A solution to the single-question crowd wisdom problem. ↩︎
Prelec, 2004. A Bayesian Truth Serum for Subjective Data. 这里的Truth Serum,直译是「真相血清」,泛指那些能让被试说真话的注射类药剂。用贝叶斯命名是因为该方法的数学证明涉及贝叶斯博弈论:信息不对称之下的博弈论。 ↩︎
原论文使用对数变换后的差、KL-散度、几何平均,并加以严格的数学证明。这里我仅做大致定性解释,从而简写为减法、「差距」、平均。 ↩︎
Weaver and Prelec, 2013. Creating Truth-Telling Incentives with the Bayesian Truth Serum ↩︎
